Grid Leak Bias or Contact Potential Bias.
There are several ways to make the correct bias for a valve. We have fixed bias, where the grid is supplied with a constant negative voltage, and automatic, or cathode bias where we bias the valve by giving the cathode a positive voltage. Since the grid always is referred to the cathode this makes the grid negative compared to the cathode and the valve gets the bias it needs. Then there is grid leak or contact potential bias, which maybe is the hardest to understand. You may ask; how can the grid be negative with respect to the cathode when there is no negative bias voltage?
The key to understand this is to look at how a valve works. To make a long story short, this is what happens: The heater heats the cathode. The cathode, when heated, makes a cloud of electrons around it, some of the electrons fall back to the cathode, but some escapes. A few of them has enough energy and the right direction to hit the grid wires, and stay there. Now the grid has more electrons than it had in the beginning, and if it were not for the grid resistor it would be negatively charged, but the grid resistor leaks this charge back to ground and the grid is maintained at the same level as before. However, if we want grid leak bias we make the grid resistor several mega ohms (5 – 20 Mohm) so there only will be a minimal current to ground. This lets the grid develop a negative charge with respect to the cathode and the grid is then negatively biased. That is the whole story……. well off course not, there is more to it. Let us take a closer look.
Grid leak bias or Contact-potential grid bias is probably the least understood of the biasing methods. In addition, in a lot of literature, and at some places on the internet, grid Leak Bias is said to be dependent on the input capacitor, and that bias develops due to charging of the capacitor. This is not quite true; the capacitor will develop a charge and maintain the bias voltage during negative alterations of the signal, but it will not alter the bias voltage developed over Rg. The bias voltage is only dependent on the grid current, and the resistor. That is unless we overdrive the stage, then some other variables also plays a role, but the grid current still is the source of the bias voltage, more about this later.
The contact potential grid current exists together with the other grid currents as described in a previous article; I will threat it here as if it were present alone. The term contact potential can have more than one meaning, dependent on who uses it. To the valve user it is a biasing mechanism inherent to the valve when we use a large resistance in the grid circuit, that is what I will discuss here, and I will call it contact potential bias (CPB). CPB is the potential that is established across a high value resistor in the external grid circuit due to the flow of electrons from the cathode, collected by the grid.
The work function of a material can be expressed as the relative ease of emitting electrons. The cathode has a low work function to ensure efficient emission, and the grid has a high work function to prevent it from emitting electrons. Work function varies between 1 and 5 volts for typical materials used in valve manufacture.
Electrons emitted from the cathode has an initial velocity related to the temperature of the cathode and its work function. Some of these electrons have enough energy to reach the grid, even though the grid is has no positive potential, and these electrons develop a retarding field. This retarding field is dependent upon the work function of the grid and any emissive material that are deposited on the grid wires, and off course on the temperature of the grid itself.
Therefore, the potential that exists as a bias between the grid and cathode does depend on the difference in work functions of the grid and cathode. The tube manufacturers did actually attempt to deposit some amount of emissive material on the grid wires during processing, to establish a work function that would reduce the contact potential value to a reasonable value. This process will continue through the valve life, and will make the contact potential bias change as the valve is used and ages. When using contact potential bias several disadvantages should be noted.
When a valve is operated with contact potential bias, the valves input resistance may no longer be in the order of thousands of Mohm but is determined by the slope of the tangent to the grid current curve at the operating bias. (The value will often be in the order of 100 – 250kohm). The result of this is that the valve is loading the input circuit more than expected.
If the valve is biased, by other means, outside the contact potential bias region, but is driven into it by positive peaks that causes grid current to flow, the signal source is also loaded, and the result could be distortion in audio amplifiers (and lowered Q when tuned circuits are involved).
When high mu triodes and sharp cutoff pentodes with limited signal handling capabilities are used, grid leak bias restricts this even more. A common mistake is to operate high mu triodes at low anode voltages, when this is done, the contact potential bias voltage may be sufficient to cut the anode current to almost zero.
When contact potential bias is used, and the only place we can use it is in low-level stages of an audio amplifier, a high value of grid resistance (5 Mohm or more) is used to hold the bias voltage. It is important to remember that the input resistance may be considerably lower than the grid resistor, and the signal handling capacity is limited to signals not much larger than 300mV if you want to make sure that you do not overload the stage, increase the grid current, and get severe distortion.
The manufacturers did try to control contact potential in the valve types commonly used in this mode, but there may anyway be considerable variations between similar valves, and during valve life span, and this must be taken into account when designing such circuits.
Now comes the question; how do we calculate the bias voltage when using contact potential bias; the answer is, it is practically impossible.
There are many variable factors that act upon this mechanism, gas current (as described in an earlier article) that drives the grid positive, and the number of electrons that have an initial velocity high enough to attract to the grid even if it does not have a positive potential are among them. How all of these factors balance out is not easy to predict, and then comes the aging of the valve as another variable. All of these factors vary even among valves of the same kind and brand.
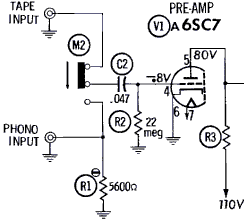
However, if we do not take all of these factors into consideration, and if we knew the grid current it would be rather easy. Let us say that the grid current for a given valve is 36 nA (0.036 uA) and the resistor is 22 Mohm, the resulting grid bias would be -0.8 Volt, just as in the schematic below, from a Fisher amplifier. In this example, this is the resulting grid current taking all factors mentioned into consideration, but the voltage given on the schematic would probably not be the same during the valves life span. In addition, if you try to measure it, your voltmeter would load the circuit so you may not read the correct grid voltage. (Even if the voltmeter has 10Mohm input resistance).
The most reliable way to check the grid bias voltage on a grid contact bias stage is to measure the voltage drop over the anode resistor, and then use the valve characteristic curves to determine what the bias voltage is. Let us look at the schematic below, B+ is 110 volts and the anode voltage is 80, so the drop over the resistor is 30 volts, the resistor is 68k. This gives us a current of: 80/68 = 1.17 mA.
A quick look at the characteristics shows that this does not add up, the grid voltage at -0.8 volts given on the schematic has to be the voltage you will measure with a voltmeter attached to the circuit, which makes sense since this is from a service manual.
I decided to do some practical tests and measurements, and made the following setup for the tests:
I also connected a signal source to the capacitor. All measurements done using a Fluke 867B. The first try was with no signal and a 6N2P-EV valve from the Voskhod factory produced in 1989. The voltage measured over Rg (Vg) was – 2 volts, and the voltage drop over Ra was 51 volts. Let us see how this confirms with the valve characteristics. 51 volts over 100k gives an anode current of 0.51 mA. As we can see in the figure below, it confirms very good with the measured value for Vg. I also tried with and without the capacitor in the circuit, and there was, off course, no difference in the voltages.

I measured with some other valves, and the results shown in the table below:
| Valve | Measured Grid voltage | Calculated Grid voltage using Ia/Va curves | Grid Current | Anode Current | Anode resistor voltage |
| 6N2P-EV Voskhod 89 | -2 | -2 | 0.35 uA | 0.51 mA | 51 |
| 6N2P-EV Voskhod 81 | -2.35 | Approx -2.2 | 0.45 uA | 0.37 mA | 37 |
| 6N2P-EV Voskhod 81 | -1.22 | 0.22 uA | 0.88 mA | 88 | |
| 6N2P-EV Voskhod 81 | -0.6 | 0.11 uA | 1.1 mA | 111 | |
| 6N1P-EV Voskhod 91 | -1.4 | Approx – 1.5 | 0.25 uA | 1.5 mA | 150 |
| 6N1P-EV Voskhod 81 | -0.7 | 0.12 uA | 1.68 mA | 168 | |
| 6N5P Nevz 68 | -0.7 | 0.12 uA | 2.02 mA | 202 | |
| 6N6P Voskhod 81 | -0.9 | 0.16 uA | 2 mA | 200 | |
| ECC83 Siemens | -1.35 | 0.24 uA | 0.11 mA | 11.1 |
The parallel resistance of the grid leak resistor (13 M) and the Fluke 867B (10M) are used when calculating the grid current. The parallel resistance is 5.65 Mohm, and this is the value used in ohms law to calculate grid current.
I also observed that connecting the Fluke 867B to the grid leak resistor did not alter the voltage over the anode resistor more than a few volts, so it probably did almost nothing to the CPB voltage on the grid.
All of these voltages measured without any signal applied to the circuit.
The table show us that the CPB voltage varies between different valves, as expected, but also between different valves of the same kind. That is also as expected due to causes mentioned before. This tells us that the grid bias, when set up as contact potential bias, will vary a lot with different valves, also off the same kind. The difference between the 6N2P-EV’s is actually 1.9 volts. The difference between the tested 6N1P’s is -0.7 volts. The variations will give a different working point (bias), even with the same valve types.
Some sources tell us that the Grid Leak Bias is dependent on the input capacitor, and the charging of it due to the signal, and that is not quite correct. The charging of the capacitor by the grid current will keep the bias of the valve stable during the negative signal cycle, and the signal voltage will, if it exceeds the CPB voltage, alter the bias by increasing the grid current. This mechanism comes into play as soon as we input a signal that is close to or larger than the Contact Potential Bias Voltage (CPB Voltage), and it leads to distortion, as I will show in a moment. First, a little look at the theory behind it. The illustrations and parts of this explanation is copied from “Neets book 6, pages 1-34 to 1-36”. Witch may be found on the internet. However, the text in Neets is, in my opinion, not correct, so I have altered parts of it.

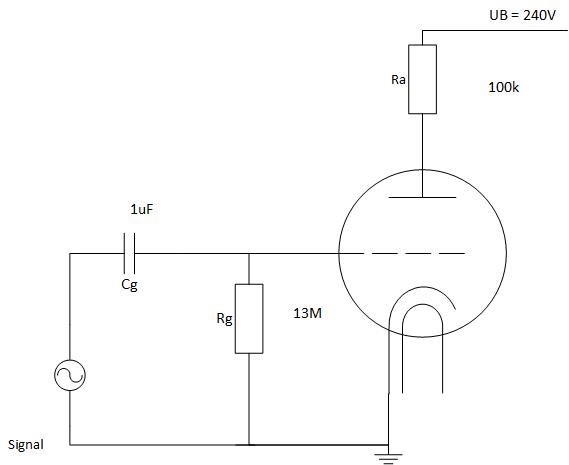
GRID-LEAK BIAS is as the name implies, bias voltage developed in the grid leg portion of the circuit. We have the grid resistor, Rg , coupling capacitor Cc, and resistance Rgk. Resistance Rgk does not exist as a physical component, but it is used to represent the internal valve resistance between the triode’s cathode and grid. Electrically, Rgk is very large, in the order of several Megaohms, but if we drive the grid positive Rgk will decrease to a quite small value, down to about 500 ohms depending on the grid current, and this is important to remember, to understand what happens when we add a signal to the circuit.
Under quiescent conditions, some conduction occurs through the valve. Some electrons will strike the wires of the grid, and a small amount of GRID CURRENT will flow through Rg to ground. There will develop a voltage over Rg as long as it has a value of 5 – 20 Mohm. This voltage is due to the contact potential difference between the cathode and the grid, this voltage will develop over Rgk even if there is no capacitor in the circuit, as long as it is not connected to any low resistance circuit, as shown in the measurements described in the text above. The grid will be kept slightly negative. This limits the number of electrons that strike the grid wires, and an equilibrium is obtained where the grid stay negative as long as there is no signal to the circuit and as long as the signal is kept below the contact potential voltage.
Now let us see what happens when we apply signal to the circuit.
In the charge figure above, the positive-going voltage at the top of Rg will be coupled to the grid causing the grid to go positive. The positively charged grid will attract more electrons from the electron stream in the tube. Grid current will flow from the grid and the negative voltage over Rg will increase, this will also affect the right-hand plate of Cc. It causes the right-hand plate to go negative. (Electrostatic repulsion from the right-hand plate of Cc will force electrons from the left-hand plate of Cc, causing it to go positive.) The electrons will flow through the signal source, to ground, from ground to the cathode, from the cathode to the grid, and finally to the right-hand plate of Cc. This charge cycle charges the Cc to the same voltage that is developed across Rg during the positive half cycle.
You may wonder why the charge current went through the valve rather than through Rg. When the grid goes positive in response to the positive-going input signal, electrostatic attraction between the grid and cathode increases. This, in turn, reduces the resistance (rgk) between the grid and cathode. Current always follows the path of least resistance. Thus, the capacitor charge path is through the valve and not through Rg.
When the first negative alternation is applied to the circuit (Discharge circuit), the left-hand plate of Cc must go negative. To do this, electrons are drawn from the right-hand plate.
The electrons travel from the right-hand plate of Cc, through Rg keeping the voltage drop over Rg negative during the negative alternation of the signal. So, Cc will discharge for the duration of the negative alternation.
BUT Cc can only discharge through Rg, which is a high-resistance path, compared to the charge path.
Remember that RC time constants and the rate of discharge increase with the size of R. Cc can therefore charge through the low resistance of rgk to its maximum negative value during the positive half-cycle. Because Cc discharges through Rg (the high resistance path), it cannot completely discharge during the duration of the negative half-cycle. As a result, at the completion of the negative alternation, Cc still retains most of the negative charge it gained during the positive alternation, and the voltage over Rg is kept nearly constant. When the next positive alternation starts, the right-hand plate of Cc will be more negative than when the first positive alternation started. During the next cycle, the same process will be repeated, with Cc charging on the positive alternation and discharging a lesser amount during the negative alternation. Therefore, at the end of the second cycle, Cc will have an even larger negative charge than it did after the first cycle.
You might think that the voltage over Rg, and thereby the charge on Cc will continue to increase until the valve is forced into cut-off. Testing show that this only will happen if the input signal is very large, but not under normal conditions. As the negative voltage over Rg and the charge on the right-hand plate of Cc keeps the grid more negative, electrostatic attraction between the grid and cathode decreases, and so does the grid current that is the source of this voltage. This, in effect, increases the resistance (Rgk) between the cathode and the grid, until Rgk becomes, in effect, the same size as Rg. At this point, the grid current decreases, charge and discharge of Cc will equal one another and the grid will remain at some negative, relatively constant voltage.
What has happened in this circuit is that Cc and Rg, with unequal charge and discharge RC time constants (paths), have acted to change the ac input to a negative dc voltage by use of the grid current. The extent of the bias on the grid will depend on several things: the amplitude of the input, the frequency of the input, the valve (grid current, contact potential), and the time constant of Rg and Cc.
This type of biasing has the advantage of being directly related to the amplitude of the input signal. If the amplitude increases, biasing increases in step with it, this in turn reduces the anode current, and thereby the amplification of the valve. We have a sort of dynamic bias that reduces the amplification if the signal get large, and increases it if the signal decreases. However, remember, the signal must be of a large enough voltage to drive the circuit into overload condition to make all of this happen, so it is not very useful, at least not in a HiFi amplifier. The main limiting factor is the amount of distortion that you may be willing to tolerate, and my testing show that the distortion rises rapidly with increasing signal voltage.
Distortion occurs during the positive alternation when the grid draws current. Current drawn from the electron stream by the grid never reaches the plate; therefore, the negative-going output is not a faithful reproduction of the input, while the positive-going output (during the negative input cycle) will be a faithful reproduction of the input, unless the signal is large enough to drive the valve into cut-off, which is unlikely during normal use.

The picture above show input and output signal to a 6N2P-ev with 37 % distortion. The output signal is at the bottom of the picture, and we clearly see that the output’s negative going alteration is the most distorted. This is also when there is grid current.
If we are going to use this type of biasing in a HiFi amplifier, we must ensure that the signal never exceeds the CPB voltage, and this voltage is dependent on the actual tube in use. As mentioned before, to use this biasing method in a HiFi amplifier, the signal should stay below 300 mV to ensure that we don’t get severe distortion, and because you actually don’t know the value of the CPB voltage due to the variations among valves.
Let us have a look at some practical tests and measurements I have done:
The table below show measurements done with some different valves. The circuit used is the same as the one used before. Distortion measured with a LEADER LDM-170 distortion meter. The input signal is 1000 Hz sine wave. < = less than.
| Input | JJ ECC83S | Mullard ECC82 | Siemens ECC83 | Siemens ECC81 | Voskhod 6N1P-EV 81 | Voskhod 6N2P-EV 81 | ||||||
| Signal
Voltage (p-p) |
-Vg | THD
% |
-Vg | THD
% |
-Vg | THD
% |
-Vg | THD
% |
-Vg | THD
% |
-Vg | THD
% |
| 0 | 0.97 | 0.86 | 0.9 | 0.7 | 0.56 | 0.69 | ||||||
| 0.4 | 1 | 0.25 | 0.87 | <0.2 | 0.9 | 0.4 | 0.8 | 0.5 | 0.57 | 0.4 | 0.78 | 0.72 |
| 0.7 | 1.1 | 1 | 1 | 0.4 | 0.95 | 1.2 | 0.88 | 1.2 | 0.68 | 0.6 | 0.87 | 1.9 |
| 0.8 | 1.17 | 2 | 1.1 | 0.8 | 1 | 2.2 | 0.9 | 1.4 | 0.71 | 0.7 | 0.9 | 2.5 |
| 1 | 1.22 | 2.6 | 1.25 | 0.9 | 1.1 | 4 | 0.97 | 2.1 | 0.8 | 0.95 | 0.97 | 2.75 |
| 1.4 | 1.4 | 6.2 | 1.3 | 1.4 | 1.2 | 7 | 1.15 | 4.1 | 0.9 | 1.25 | 1.13 | 7.2 |
| 1.8 | 1.5 | 11 | 1.4 | 2 | 1.35 | 12.8 | 1.3 | 6.3 | 1 | 2.35 | 1.2 | 9.5 |
| 2 | 1.6 | 15 | 1.5 | 2.2 | 1.4 | 17.5 | 1.4 | 8 | 1.18 | 2.6 | 1.4 | 16.5 |
| 2.5 | 1.8 | 26 | 1.7 | 3.2 | 1.65 | 34 | 1.5 | 11 | 1.4 | 4.8 | 1.65 | 27.5 |
| 3 | 2.0 | – | 1.9 | 3.8 | 1.8 | – | 1.8 | 15 | 1.6 | 6.4 | 1.8 | 37 |
If we look at –Vg in the table, we clearly see that the grid voltage increases (gets more negative) with increasing signal voltage.
What we also see is that the valves with the highest amplification factor (u) gives much higher distortion than valves with lower amplification factor, and this is normal. The output signal from the ECC83/6N2P-EV is more distorted, but is also much larger than the output signal from the valves with lower amplification.
JJ ECC 83S is the only current production valve measured, and it measures very similar to the other ECC83/12AX7 types tested (Siemens ECC83 and 6N2P-EV).
The valve with the highest distortion measured is in fact Siemens ECC83. This is (I believe) an Ei produced valve labelled Siemens, in the other end of the scale is Mullard ECC82, which has the lowest distortion, followed by 6N1P-EV as the second best regarding distortion.
JJ ECC83S measured surprisingly low distortion with 0.4 v signal, but rises rapidly as the signal gets larger.
This confirms what I said earlier considering high “mu” valves.
The voltage at 0 signal is the CPB voltage. The CPB voltage develops as soon as the heater is starting and is not dependent on the anode voltage.
The signal voltages are peak-to-peak voltage; to convert this to rms we use the formula:
Vrms = 0.3535 * Vpp
0.4 volts p-p = 0.14 Vrms, 0.7 Vp-p = 0.247 Vrms and 0.8 Vp-p = 0.282 Vrms.
To summarize:
The Grid Leak Bias voltage is only dependent on the voltage drop the grid current makes over Rg. It is not dependent on the capacitor and the charge and discharge of it. The capacitor charge only helps to keep the voltage almost constant over Rg during the negative alteration of the signal voltage. If the signal exceeds the contact potential voltage the grid current increases, and so does the voltage drop over Rg, but when this happens the distortion rises rapidly and makes this type of biasing useless for signal levels that is larger than or equal to the Contact Potential Voltage. At least for HiFi amplifiers where the level of distortion that occurs is unacceptable.
One last comment:
If we drive, a normal biased stage into overdrive by allowing a signal that is larger than the grid bias voltage the stage will off course start to draw grid current, in the same manner as a CPB stage, and distortion will occur. However, as long as we stick to the manufacturers recommendations regarding maximum value for Rg, it will not develop a large negative voltage on the grid for a longer period, this because the grid current will “leak” to ground through Rg.
Although it has been used in some rather successful RIAA amplifiers, and as input stages for low-level signals from microphones. Grid leak bias, or contact potential bias gives a rather unpredictable bias point for the valve, and is, in my opinion, not the biasing method to choose for a HiFi amplifier.

First thank you very much for a very comprehensive reseach about this fenoma.
Do you think this contact potential current & voltage differs conciderebly in hi mu frame grid tubes, like Tesla E83CC, TFK ECC803S & E283CC. (They look from outside more like ECC88’s)
The TFK ECC803S (frame grid) reputation & price has gone through the roof! To confuse things even more, both AEG & Tesla/JJ ECC803S are long plates, but Tesla E83CC & JJ ECC83 are frame grid types.
There must be a real technical reason these (specially TFK) are prefered by so many listeners. I’ve considered grid current reason involved, even still biased in the “no grid current area”
The grid must be more out of the space charge cloud in this high mu type of design. The data sheets for Tesla & TFK frame grid versions seems just to be copies of their earlier long plate designs, but the Philips E283CC shows a little different figures and max 25MOhm for grid current bias.
How does the contact potential current behave when you bias conciderably above this voltage with f.ex. a cathode resistor? Is the same CPC still flowing through the grid leak, or is it decreasing next to zero?
Is there any influence of the anode voltage to the grid leak current at the same current if biased above the CPV?
Many questions, but very intresing field to investigate.
Hi,
Yes, it is an interesting field to explore.
The contact potential voltage depends on the material used for the cathode and the grid, to be more specific, the potential generated by two metals in contact or substantially close to each other in air or vacuum. the potential depends on the work function of the materials used (or the surfaces of the materials and the heating of these), and I don’t think that a frame grid valve would be any different regarding this. The contact potential voltage will add to the grid voltage set by the bias, if the resistance in the grid circuit is large enough so that the cp voltage can build up over the grid resistor.
The current due to the contact potential voltage is an extremely small current, and you need a very high resistance in the grid circuit for the contact potential voltage to remain at the grid, and don’t “leak” to ground.
TFK ECC803S is among the finest valves ever produced, it has low microphonics, very low noise and the two sections are very well matched, but it was produced in a very limited quantity and are practically impossible to obtain today, and if you find it the price is extremely high.
The measurements I have done sow far, show no influence of the anode voltage on the grid leak current, it also seems to be independent of how the grid is biased. But remember, as said before, it is an extremely small current.
What is very different when you look at a frame grid valve is, of course the frame grid itself, which is very tightly and precisely wound, and with a very thin wire, but also that the distance between the cathode and the grid is very small compared to a “normal” valve. Both these things together should give us a valve with a relatively high gm. ECC88 has a gm of 12,5 ma/volt.
The tight and precise winding of the very thin grid wire in a frame grid valve will in most cases give us a valve with very smooth and linear curves and thereby, theoretically, less distortion than a valve with an “normal” grid, and this may be one of the reasons why these valves are preferred by many.
But as said before, it is a very interesting subject an I will try to test some frame grid valves and compare these to “normal” valves to see if there is any measurable difference when regarding the contact potential voltage, and other parameters measured and publish the results here.
Amazing body of work. I have not seen such in depth discussion of hollow state since college in the early 1960s. Thank you for the engineering level presentation.
I linked your page on “contact potential bias” in a discussion of vintage amateur radio gear. I hope the brief quote is OK.
https://wireless-girl.com/Projects/AMTransmitters/HeathkitDX60.html
“For more information, consult this web site:
https://tubes.njunis.net/?p=256&lang=en
Which states:
“The manufacturers did try to control contact potential in the valve types commonly used in this mode, but there may anyway be considerable variations between similar valves, and during valve life span, and this must be taken into account when designing such circuits. Now comes the question; how do we calculate the bias voltage when using contact potential bias; the answer is, it is practically impossible. If the valve is biased, by other means, outside the contact potential bias region, but is driven into it by positive peaks that causes grid current to flow, the signal source is also loaded, and the result could be distortion in audio amplifiers.” This is particularly important, considering the proliferation of Chinese tubes these days.”
Thank you for the nice words. It is perfectly fine for you to use this as long as you keep the reference to my page
What are the effects of different value grid leak resistors? I see 5-20M as a common range. The Bogen CH-18 I have uses a 1M grid leak for a 6SF5
Hi, different values of grid leak resistors are not going to make much of a difference, as long as it is large enough, in the order of 5 – 20 Mohms. 1 M grid leak resistor is a very small value to be used in a grid leak biased system, but it has been used in several PA amplifiers for mic. input. The 1 M resistor will make a very low bias voltage, almost “zero” bias. But it is used as a mic input, and the microphone signals usually has a very low value, in the order of 0.001 to 0.01 volt so it should not be of any problem. If you are going to use this input for something other than a mic, I would suggest that you modify the input circuit to a ordinary biased stage with a cathode resistor.