A bit about Single ended stages, and output transformers.
I recommend that the article impedance matching of loudspeakers to output valves is read first. It will give some useful basic knowledge about the subject.
I also recommend to read the article: Difference between power valves and voltage amplifying valves
In this article I will give some more formulas and explanations about the subject, that was not presented in the first article.
Unless otherwise noted most of the subjects presented here can be applied for push-pull output stages.
Single ended stages are always class A, anything else would give severe distortion.
In this article I will deal with class A stages where there is no grid current, that is the peaks of the input signal will always be less than the negative grid voltage. This is called class A1.
I always use Za for the load to the valve, anode external load, this is because the load to an output stage is a loudspeaker and not a resistance. The load is always an impedance consisting of inductive and capacitive loading in addition to some resistive load. I also use ri for the valve’s internal resistance, it is in many books called ra (anode resistance (Europe)) or rp (plate resistance (US)).
Let us start with the anode efficiency:
That is how much of the power in from the power supply we actually get out of the stage as signal power, the rest will mostly be radiated as heat. There is a formula for this, we assume that the load is a pure resistance:

This is a very simple formula, Po is signal power out to the load, and Pin is DC power delivered from the power supply and the 100 gives us the result in %. The theoretical maximum efficiency for a class A1 single ended stage is 50 %, and that value will never be reached in real life.
The maximum efficiency of a triode class A1 stage is about 25 percent, and that is rarely reached, but somewhere between 15 and 25% is realistic to achieve with triodes. What puts a limit is that we will seldom use the whole range of the load line because of the curving of the characteristics, it would lead to severe distortion.
The maximum output from a pentode or a beam tetrode is another story These valves are more efficient than triodes due to the shapes of their Va – Ia characteristics. The zero-bias point on the pentode characteristics is much closer to the axis for zero volt on the anode, and thereby permit us to operate a lot closer to 0 volt on the anode without severe distortion, compared to a triode. These valves can utilize efficiencies of 35 – 45 % for a single ended class A1 stage. And what does that mean, well, for a triode with allowed anode dissipation of 15 w, the most we can get out of it is 25 %, which is about 3.5 watts, but for a pentode with 15-watt anode dissipation we can get almost 6.5 watts.
Optimum load presented to valves, and a little bit about distortion:

Single ended triode stage.
The distortion in a class A single ended triode amplifier is almost entirely 2 harmonics. A compromise between maximum power output and distortion can be obtained by careful selection of ac load impedance (Za) and operation point for the valve. As a general rule the best AC load impedance for a single ended triode stage will be approximately when Za = 2 x ri. The curves in the figure below illustrate how the distortion and power out and ratio of Za/ri are related for a typical single ended class A amplifier.
In all power valves, well actually all valves, maximum power output will occur when Za = ri, but with a triode this will not give us what we may call “the maximum undistorted power output”, that is in most cases be obtained when Za is approximately 2 x ri. The power output when Za is 2xri, will be in the order of 90% of the absolute maximum (Za=ri) so we lose only 10% power to get a much better distortion factor. If you think that this does not match the curves in the figure below, remember that these are drawn for a specific level of distortion.

The figure shows us that for any given value of distortion, the maximum output power is obtained when the ac load impedance, Za, is approximately equal to 2 x ri. The chosen operating point is also important for the choice of load impedance. The best operating conditions for the valve are found by doing a series of graphical experiments.
For the wanted supply voltage, which should be equal or less than the highest rated voltage for the valve, we locate on the characteristics the anode current which gives us the max rated anode dissipation. In the figure below this is point 0a, at this point ri is 2250 ohms. To illustrate how the power output varies with chosen ratio of Za/ri, there is three load lines in the figure. Load line A has been drawn through point 0a for Za = 2250 ohms, that is Za/ri=1. Load lines B and C is drawn for Za/ri=2. The length of the load lines shows the anode current and voltage variation that will give about 5% distortion. It is evident from the load lines that load lines B and C, where Za/ri is 2, gives the largest current and voltage variations, and thereby most power output. Load line C has an operating point less than the stated maximum for the valve, but still gives us almost the same power output as load line B, and if we do some calculations, it will show a slightly better efficiency than load line B. therefore it sometimes can be desirable to choose an operating point slightly below the maximum rated value, it will also give less stress on the valve and in most cases make the lifetime a bit longer.

The conclusion on the triode stage regarding finding optimum load is that we use a load for the valve that is approximately 2 times the internal resistance (ri, ra, or rp) at the operating point. And remember, although the internal resistance varies with the anode current, the variations are relatively small in the actual region of the operating point, for a class A1 single ended output stage.

Single ended pentode stage.
Now let us look at the pentode/beam tetrode single ended stage, it is in many ways a very different story. I will use the 6L6 beam tetrode as the example, because there are a lot of data available on this valve.
The main advantage in using pentodes and beam tetrodes instead of triodes in a single ended output stage are that we can get higher efficiencies and use less grid drive voltages for the same output power. As mentioned before: The zero-bias point on the pentode characteristics is much closer to the axis for zero volt on the anode, and thereby permit us to operate a lot closer to 0 volt on the anode without severe distortion.
The figure below shows typical behaviour of a single ended pentode/beam tetrode when used as a single ended output stage. This is very different from the distortion, power output and load triode curves shown above.

The power out curve show us that max power out occurs when the load is about ri/6. Minimum distortion occurs at a value a little less than this. The pentode class A1 stage has more distortion than a similar triode stage, this is primary due to the 3. Harmonic distortion, especially when operating around the maximum power region. This can be limited by careful selection of operating point and load to the valve, at the expense of slightly less power out. A general relationship for the optimum load to a pentode or beam tetrode can be expressed as:

As shown in the figure above, changing the load will also make a large change in the distortion, not only in THD but also in the spectrum of the distortion, with a load of ri/6 the distortion is mainly 3 harmonics. But when we take it all the way down to ri/12 the distortion is dominated by the 2 harmonics, and the thd rises from about 8 % to almost 12 . Ri/6 is considered to be almost the optimum load for a 6l6 single ended amp, at least when it comes to maximum power out, and ri/12 is probably a bit too heavy loading of the valve, but by using a load different from ri/6 we can still get low distortion, and we can alter the load to get a different distortion spectrum, and thereby change the sound of the amplifier considerably.
The optimum value for Za can be found by making an ac load line that passes through the operating point, determined by the maximum anode voltage, anode dissipation and the knee of the zero-bias curve. An example is shown in the figure below.

There is also another way to do this, I will explain briefly how:
With the triode we saw that the factor Za/ri plays a crucial role. With pentodes/beam tetrodes the vg curves are almost horizontal and that indicates that the internal resistance, ri, is much higher than the load resistance Za. This tell us that the factor Za/ri is useless for pentodes. It is possible to use the pentode DC internal resistance in this type of calculations, Za/Ri should for a practical pentode have a value of 0.75 to 1.00 (one is for a theoretical perfect pentode).
These calculations are relatively simple, first we have to find the DC internal resistance at the quiescent point. This is indicated by the red lines in the 6l6 characteristics above. The quiescent point is at Ia 0 = 76 mA and the anode voltage is at 250 volts. This gives us a DC internal resistance at:
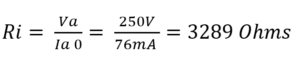
This gives us a DC internal resistance of 3289 ohms, 3000 to 3500 ohms load is around the load values that are used in many 6l6 SE amplifiers . But let us calculate Za using the factor mentioned above, as said before this should be between 0.75 to 1.0 times Ri, here we can calculate with different factors, and plot this in the characteristics to find which factor that gives us the maximum power out, and as little distortion as possible. But I am not going to do that here, I’ll take a shortcut as follows:
The factor 1 is for an ideal pentode, and if we use that value, it would be within the limits (ri/12 – ri/6) set above, but since the valve is not perfect we can assume the factor should be below that. 0.9 is a good starting point since this is a beam tetrode. (With a pentode I would go for a factor of 0.85) and I will use that. Then Za should be:
![]()
And this is within the limits set above (approx. ri/7.6)
We should also take precautions to avoid excessive screen grid dissipation. The screen grid dissipation is equal to the product of the average screen current and the screen grid to cathode voltage. It will not be treated any further here.
The transformer, and why the primary side should have a large inductive value.
It is well known that the primary of an output transformer should have a relatively large inductive value, expressed in Henrys (H), to give a good low frequency response, but why is it so?
This is about the transformer, and is valid whether you use a triode or pentode in the output stage, and also for push-pull stages.
I will try to explain this by using the figure below:

The figure shows a triode connected to a loudspeaker using a transformer, and the load to the valve then becomes:
![]()
Where N is the turns ratio of the transformer. This load is shown in broken lines in the drawing above. The drawing also show that this resistor is in parallel to the primary winding. Any coil or transformer winding has an inductive reactance Xp that is dependent on the frequency, and the value of the coil, Lp in the drawing. To make sure that the load presented to the valve is close to the reflected impedance Za, the inductive reactance, Xp, must have a high value to not interfere considerably with the reflected value Za.
An example will make this easier to understand.
Let us say that the transformer gives us a reflected load of 6600 ohms. And the transformer primary has a value (Lp) of 15 H. Now let us calculate the reactance of the primary winding at 50 Hz:
![]()
This value will then be in parallel with the reflected impedance of 6600 ohms. The actual Valve load at 50Hz will then be:

The effective load will be less than half the reflected, and wanted, value. This will make the response at the low frequencies drop considerably, due to the increased loading of the valve. The Inductive reactance increases with frequency, in this case it will be 376 991 ohms at 4000 Hz, and will not be problematic at that frequency.
Let us see what happens if we increase the inductance to 88 H:
![]()
And the parallel connection:

This is a much better result and show us that the frequency response curve will still fall of a bit, but this will probably be an acceptable response.
There is also another reason for using a large inductance at the primary, the signal current in the valve will increase due to the low value load, and it might even increase beyond the maximum allowable current for the valve. This will decrease the lifetime of the valve, and it can also be the cause of amplitude distortion.
But there are many considerations to take when selecting an output transformer, the primary inductance is only one of them. The transformer will always be a compromise between a lot of parameters, but that is not to be written about in this article.

Comments
A bit about Single ended stages, and output transformers. — No Comments
HTML tags allowed in your comment: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>