Impedance matching of loudspeakers to output valves.
This is a simplified approach, just to explain how it works.
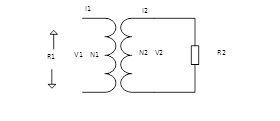
A loudspeaker usually has an impedance of 4 – 8 ohms, and an output valve will usually demand a load of several k.ohms. To make this work we need a transformer to match the low impedance loudspeaker to the high impedance tube.
I will assume an ideal transformer, with no loss or capacitance; it will be close enough to the real thing.
If we see this as an ideal transformer (no loss), we can use the following expression:
V1/N1 = V2/N2
By adding that the primary power equals the secondary power, we can use the following:
n = N1/N2 = √(R1/R2)
Where:
N1 = number of turns on primary
N2 = Number of turns on secondary
R2 = Load impedance on secondary side (loudspeaker)
R1 = Impact of R2 reflected over to the primary side (plate load)
n = the transformer ratio
Let us look at an example to clarify:
(Example taken from an old textbook, I used when I was at school (a long time ago..))
We will use a power pentode as an output stage in a SE amp.
Plate voltage is 250V, Grid has a signal level of 5 V, the load on the tube (Rl) should be 5.2 K.
The available transformer has a ratio: N1/N2 = 36. We see the transformer as ideal. (At this moment)
Loudspeaker impedance needed with the available transformer:
N1/N2 = √(R1/R2)
R2 is the loadspeaker impedance, R1 (Rl) is the optimum load impedance, by solving for R2:
R2= R1/(N1/N2)²=5200/(36) ² =5200/1296 = 4.02 ohm
If the manufacturer gives the impedance ratio (in this case 5200 to 4 ohms, we would determine the ratio as √(5200/4)=36, so this transformer would give us a 5.2 k load on the tube if we use a 4 ohm speaker, but what if we were to use an 8 ohm speaker with the same transformer?
The ratio will be the same, 36, but the transformer would present a different load to the valve:
√(R1/R2)=36 => √(R1/8)=36
Solve for R1 (anode load):
R1 = (n) ² x R2 => (36) ² x 8 = 10368 ohm would be the load reflected to the valve if we used an 8-ohm speaker on the same transformer.
Witch off course is twice the load reflected for a 4-ohm speaker, but here is the math to prove it.
Primary DC resistance:
Now let us see what happens if we do not see the transformer as ideal, let us introduce the dc resistance to the case:
When ac signal is present, the valve will see the dc resistance of the primary turns of the transformer in series with the reflected impedance from the load. Let me take an example:
Dc resistance of coil is 300 ohm (Rpri); with no signal present, the valve will see a 300-ohm resistance. This resistance is the one we will use for the DC load line in the curves. But, as soon as the signal is present this resistance will appear in series with the reflected impedance, using the same transformer as above this means (4 ohm load) that the total impedance that the tube sees is 300 + 5200 ohm = 5500 0hms. The difference by taking primary dc resistance into the equations is less than 10% so it is not going to make any big difference, the tolerances between valves is in most cases larger than this, but it might be important if we want to plot the DC load line. That is not the whole story; let us look at:
Power loss and plate load impedance with a non-ideal transformer:
The secondary side does also have a dc resistance, and we must to consider this to if we want to find the power loss in the transformer, and the total impedance the anode sees. The DC resistance of the secondary will be reflected over to the primary side by the transformer. The DC resistance of the primary side is usually rather small, about 0.2 – 0.5 ohms is a normal value, but it will be reflected over by the transformer ratio. Let’s take a look at the math:
Rpri is the primary DC resistance
Rsec is the secondary DC resistance
Rpri= 300 ohm (yes it is a bit high)
Rsec= 0.2 ohm
The secondary Dc resistance reflected to the primary is then:
n ² x Rpri => 36 ² x 0.2 = 259 ohm
The total copper resistance the tube sees is:
Rtot= Rpri + (n ² x Rsec) = > 300 + (36 ² x 0.2) = 559 Ohm. This is important if we are going to find the power loss in a non-ideal transformer.
The primary losses (and that includes the reflected Rsec):
(Rtot/Rtot+R1) x 100%= (559/559+5200) x 100 = 9.7 % (not a very good transformer)
The iron loss typically is about 5% so this transformer gives a total loss of 14.7 %, then the power efficiency is about 85%. That is not a very good figure; a good output transformer should have power efficiencies between 90 and 95%.
Plate load impedance with a non-ideal transformer:
To calculate the anode load with a non-ideal transformer we have to include all of the loss resistances mentioned above, and R2 (anode load) from the first figure:
The simplified equation above, with no loss, looks like this:
R1 = (n) ² x R2 => (36) ² x 4 = 5200
The equation with a non-ideal transformer will be:
R1 = Rpri + (n ² x Rsec) + (n ² x R2) => 300 + (36 ² + 0.2) + (36 ² x 4) = 5743.2 ohm
It is less than 15% off from the simplified equation, and, in my opinion, the simplified equation is accurate enough, due to manufacturing tolerances. Unless, of course, we plot the curves for the actual valve, measures the transformer, and then use these values for calculations, but then, we have to redo the whole thing if we have to replace valves.
There are other important parameters to consider when choosing a transformer, such as; primary self-inductance and the capacitance of the transformer windings, but I am not going to write about it at this moment.
The text above is mainly written for a SE stage, but it is also valid for Push Pull. If using a PP stage remember that, the primary winding is divided into two halves and these have an opposite winding direction. Each of them has o.5xN1 windings and the loss resistance is 0.5xRpri. I will not look any deeper into it here, but maybe write a bit about it later if there is interest for it.
The text, and equations, are valid for any transformer-based stage, the impedance and resistance values will be different if we use it for an interstage transformer, but the principles are the same.


Pingback:Output transformers and push-pull stages. – tubes
Thank you for this explanation. Could you write a bit of math for the Push Pull stage?
Hi and thank you for your comment. I will publish a new article about push-pull stages soon, but the math is almost the same. The primary is calculated as anode to anode, and the secondary the same way as in a single ended stage. More about this in the upcoming article.