Før vi begynner må vi være klar over hva en kondensator egentlig er; Vi  kan betrakte den som to metallobjekter med en isolator mellom. Så enkelt er det. Derfor vil det alltid være kapasitans mellom elementene i et rør. Et rør er faktisk laget av noen metallobjekter med en isolator mellom. Isolatoren i et rør er selvfølgelig vakuum. I denne teksten vil jeg bare se på de interne kapasitetene i selve røret, og ikke vurdere noen kapasitanser i eksterne ledninger eller tilkoblinger, dette er umulig å beregne fordi de alltid vil være avhengig av forsterkerens fysiske utforming. Så la oss se på røret, se hvor kapasitansene er, og hvilken innvirkning de har på bruken av røret.

Triode.

Trioden består av tre elektroder, katode, gitter og anode, og disse er forskjellige elektriske ledere med isolator mellom, derfor må også være kapasitans mellom dem. Vi regner vanligvis med tre kondensatorer i en triode; gitter til anode kondensatoren, Cga, gitter til katode kondensatoren, Cgk og anode til katode kondensatoren, Cak. Vi visualiserer dem slik:

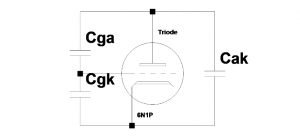
Disse kapasitansene er uønskede; vi kaller dem parasittiske kapasiteter, og produsentene gjorde alt de kunne for å minimere dem. En annen måte å tegne dem på er slik:

I denne tegningen kan vi se at Cgk er i inngangskretsen, og at Cak er i utgangskretsen. Cga er mellom inngangs- og utgangskretsen, så den vil derfor påvirke både inngangs- og utgangs kapasiteten til triode kretsen.

Cak er vekselspenningsmessig i parallell med anodebelastningen. Den vil påvirke kretsen så snart frekvensen blir høy nok til at dens reaktans nærmer seg samme verdi som anodebelastningen. Da vil forsterkningen gradvis minke etter hvert som reaktansen minker, altså når frekvensen øker.

La meg vise hvordan dette ser ut, jeg har endret en spice modell for 6N1P-EV, i den opprinnelige modellen Cak er 1,6pF og frekvens plottet fra LTSpice ser slik ut:

Vi ser at trinnets forsterkning er konstant over 100 kHz.

La oss nå prøve den endrede modellen, med Cak satt til 150 pF (jeg kunne bare ha satt en kondensator parallelt med røret, anode til katode, men jeg ønsket også å teste spicemodellen.):

Her kan vi se at forsterkningen begynner å minke litt ved ca 30 kHz, og faller litt av på grunn av den høye verdien på Cak. Trinnets totale belastning var 6875 ohm. (Ra 22k og last 10k) 150pF verdien brukt til Cak her er ikke særlig realistisk, men kun for å illustrere hvordan det fungerer. Cak vil sjelden gi noen problemer ved audiofrekvenser, men bør tas i betraktning ved frekvenser i MHz-området.

Utgangskapasitansen til en triodekrets består imidlertid ikke av Cak alene, vi har også Cga koblet til anoden, og den har en viss innflytelse. Uten å ta med hele den matematiske utregningen, er formelen for utgangskapasitans:

Hvor A er dynamisk forsterkning  =

Vi kan se at utgangskapasitansen ikke er veldig påvirket av forsterkningen fordi:

Cak i 6N1P-EV er 1,6 pF og har ved 10 MHz en reaktans på ca. 9950 ohm.

Formelen for en kondensators reaktans er:

La oss nå se på Cgk, denne kondensatoren er over inngangen til røret og vil derfor fungere som en belastning på signalkilden. Den vil være i serie med signalkildens interne motstand. Som vist i figuren nedenfor:

Katodekondensatoren Ck har svært liten reaktans i lydfrekvensene, så vi anser den som en kortslutning. Ri (signalkildens interne motstand) og Cgk danner en spenningsdeler for signalspenningen. Etter hvert som frekvensen øker, og Cgk-reaktansen minker, vil mindre av signalspenningen bli presentert over Cgk og dermed til røret. En høy verdi av Ri vil få dette til å skje ved en lavere frekvens, og signalspenningen til røret reduseres noe som gir minkende utsignal. Cgk har en typisk verdi på et par pF vil trolig ikke gi noen problemer ved audiofrekvenser, men kan være verdt å vurdere når du designer en filterkrets, og selvfølgelig på radiofrekvenser.

La oss nå se på Cga, som er kondensatoren som har størst innflytelse på forsterkertrinnet. Dette skyldes hovedsakelig at den befinner seg mellom anodekretsen (utgangskrets) og inngangskretsen. Dette gjør at den har stor innvirkning kretsens inngangskapasitans. La oss se nærmere på dette, med en resistiv (ren motstand) last på røret, som i figuren nedenfor:

Følgende vil bli brukt i denne forklaringen:

A = Dynamisk forsterkning

Xcgk = Cgk reaktans,

Xcga = Cga reaktans

Anode veksel spenningen Ua er i motsatt fase av vekselspenningen på inngangen Vg, og opptrer over en seriell forbindelse av Cgk og Cga, som i figuren nedenfor.

Vi får da:

Dette betyr at spenningene over Cgk og Cga er i motsatt fase, og at spenningen over Cga er (1 + A) ganger større enn spenningen over Cgk. Strømmen gjennom Cgk (I1) er 90 grader foran Vg, og strømmen gjennom Cga (I2) er 90 grader foran Vcga. I1 og I2 er da i motsatt fase, så når I1 flyter ned flyter I2 opp, som vist med pilene i tegningen ovenfor.

Ved å bruke Kirchhoffs lov kan vi finne at den totale gjeldende strøm, ig, i gitter kretsen er:

(Kirchoffs lover kan finnes her)

Og dette kan skrives som:

Og her kunne jeg skrive en lang matematisk utredning som til slutt vil lede oss til en formel for inngangskapasitansen til røret når signalet er koblet mellom gitteret og katoden:

Alternativt:

som faktisk er den samme formelen.

Konklusjonen er at rørets inngangskapasitans er mye større enn Cgk og Cga alene. Den er avhengig av forsterkningen (A) som avhenger av μ og Ra. Mer forsterkning i en krets betyr høyere inngangskapasitans, og inngangskapasitansen er for det meste avhengig av Cga og forsterkningen. Inngangskapasitansen øker med forsterkningen med faktoren: (1 + A) ≈A. Dette er kjent som «Miller-effekten».

La oss ta et eksempel:

Rør: 6N1P-EV

Cgk = 3,2 pF

CGA = 2.7pF

Ug = – 4,2 v

Ri = 7,5 k

Ua = 300 v

μ (A) = 35,7

Cin = 83,63pF

Som er en betydelig større verdi enn både Cga og Cgk, og bør tas med i betraktning ved utforming av et forsterkertrinn. Inngangs kapasitansen kan også være noe problematisk hvis anodebelastningen er reaktiv, nøkkelordet her er resonans.

Alle de ovennevnte beregningene gjelder for en grunnleggende felles katodekrets, slik:

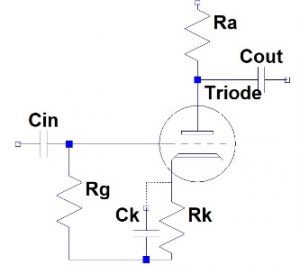
Katodefølgeren har også en viss inngangskapasitans, men når du bruker en katodefølger, har utgangskapasiteten (Cak) i praksis ingen innflytelse. Katodefølgeren (eller anodekretsen) ser slik ut:

Formelen for inngangskapasitansen er (uten all matematikken som fører fram til formelen):

Til slutt, hvis du vil bruke en «felles gitter» kopling, er inngangskapasitansen:

Og utgang:

La oss se på Tetroden og Pentoden:

En av grunnene til utviklingen av tetroden og pentoden var den høye inngangskapasitansen til Trioden, og problemene det forårsaket, spesielt ved radiofrekvenser.

Dette er interelektrode kapasitetene til en tetrode:

Hvis skjermgitteret er effektivt avkoblet til jord, kan dette forenkles. De to kapasitetene mellom kontrollgitter og katode, samt kontrollgitter og skjermgitter er parallelle, og kapasitetene mellom anode og katode, skjerm og anode er også parallelle. Vi kan da tegne det slik:

Inngang som alltid på venstre side og utgang på høyre side.

Gitter til anodekapasiteten, Cga, til en tetrode eller pentode er vanligvis i størrelsesorden 0,005pF, og dette gjør at vi  unngår problemene med inngangskapasitans som vi har i triode kretser, selv om vi fortsatt har «Miller-effekten» i både tetrode- og pentode kretser.

La oss se på kapasitansene i en pentode:

Tegningen viser at det er veldig mange forskjellige kapasitanser i en pentode, men heldigvis er kan vi forenkle dette betraktelig. Fanggitteret (g3) er koblet til katoden og skjermgitteret (g2) har vanligvis en stor kondensator til jord, med mindre det er i ultralinær kopling. Så disse kapasitansene er uvesentlige. Dette gir oss egentlig samme kapasitanser som i en triode, Cg1k, Cg1a og Cak.

På samme måte som i en triode vil Miller-effekten øke inngangskapasitansen med en faktor som avhenger av forsterkningen, men fanggitteret er jordet (koblet til katoden) slik at dette vil hjelpe, det vil redusere Cga med en faktor som også er avhengig av forsterkningen, og netto inngangskapasitans vil forbli lav. For alle praktiske formål kan vi glemme Miller-effekten for pentoder, i hvert fall når det gjelder lydfrekvenser.

For Pentoden, (vanlig katodekobling) har vi da:

Inngangskapasitans:

Utgangskapasitans:

c_out = Cak

Det er slutten på denne lille innføringen i rørkapasitanser, uten for mye matematikk involvert.