Dette er en forenklet tilnærming, bare for å forklare hvordan det fungerer.

Prinsippene og beregningene er i utgangspunktet de samme for et push pull-trinn som for et SE-trinn, så alt som er beskrevet i  Impedanstilpasning av rørforsterkere til høyttalere. artikkelen er gyldig for enhver transformator, men det er andre ting å ta hensyn til når du beregner en push-pull-transformator. La meg imidlertid se litt på beregningene og transformatoren, før vi ser på selve utgangstrinnet.

Når man skal  bruke formlene for å beregne transformatorer er det viktig å huske at en utgangstransformator ikke har noen impedans i seg selv; den reflekterer impedansen og eventuelle motstander på sekundærsiden over til primærsiden og presenterer derved en impedans som en belastning til utgangsrørene.

Lasten til rør i et push-pull-trinn er alltid spesifisert som «anode til anode» (Zaa) illustrert på tegningen nedenfor. Fordi  B + er AC-jord, ser hvert rør faktisk en belastningsimpedans som er Zaa / 4, under forutsetning av at bare ett rør leder strøm igjennom trafoen. Dersom begge rørene leder vil begge delene av trafoen lede strøm og belastningsforholdene blir påvirket av dette.

Nå som vi har etablert hvordan vi skal spesifisere belastningen, la oss se på formlene for beregning av transformatoren. Nøkkelfaktoren er som alltid omsetningsforholdet til transformatoren. Det er forholdet mellom antall viklinger på primærsiden dividert med antall viklinger på sekundærsiden, som tilsvarer spenningen på primærsiden dividert på spenningen på sekundærsiden, og til slutt kvadratroten til den reflekterte impedansen på primærsiden dividert på impedansen på sekundærsiden, og vi kunne selvfølgelig også bruke strømmen, så i en formel ser det slik ut:

n = N1 / N2 = V1 / V2 = √ (R1 / R2) = Ip / Is

Som før:

N1 = antall viklinger på primærsiden (også Np)

N2 = Antall viklinger på sekundærsiden (også Ns)

V1 = Spenning på primærsiden

V2 = Spenning på sekundærsiden

R2 = Lastimpedans på sekundærsiden (høyttaler)

R1 = Effekt av R2 reflektert over til sekundærsiden (her: anode-til-anodebelastning)

Ip = primær vekselstrøm

Is = Sekundær vekselstrøm

n = transformatorens omsetningsforhold

Alle verdiene illustrert nedenfor:

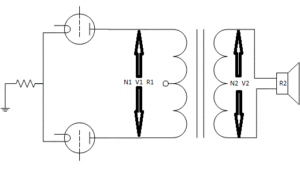
En av de vanlige situasjonene er at vi ønsker å beregne belastningen en gitt transformator gir til rørene. Så la oss se på disse beregningene.

Spesifikasjonene for Toroidy-transformatoren uten den primære impedansen er:

Tekniske data

Beregnet for Push-Pull:

Toroidal kjernetype

Ultralinær tapping 43%

Nominell effekt 50W

Nominell anodestrøm 200 mA

Frekvensbåndbredde (-3dB) 8 Hz – 54 kHz

Sekundær impedans 4 og 8 Ω

Primær impedans

Turns Ratio (Np: Ns) 40,62: 1 (4Ω), 28,72: 1 (8Ω)

Primær induktans Lp 591 H

Primær lekkasjeinduktans Lsp 3,5 mH

Total primær DC-motstand 96,1 Ω

Effektiv primærkapasitet 11,2 nF

Mål (standard) 115 mm (OD) x 65 mm (h), vekt: 2,7 kg

Mål EXPO 120 mm (OD) x 80 mm (h), vekt: 4,4 kg

La oss nå beregne den primære impedansen til denne transformatoren, vi kan velge 8 eller 4 ohm sekundær utgang for beregningene, den primære skal uansett være den samme:

Formelen løst for R1 (primær impedans) er:

R1 = (n) ² x R2 => (28,72) ² x 8 = 6598,7 ohm anode til anode. (Hvis det løses for R2 = 4 ohm, får vi 6599,9)

Imidlertid kunne vi, hvis ønsket, bruke 4-ohm-tappingen koblet til en 8-ohm-høyttaler, og hva ville belastningen på rørene da være? Ved 4 ohm belastning har vi et omsetningsforhold på 40,62, så den beregnede verdien vil være:

R1 = (n) ² x R2 => (40,62) ² x 8 = 13 199,9 ohm.

Det betyr at hvis vi bruker 4-ohm-tappingen for en 8-ohm-høyttaler, ville den samme transformatoren gi en reflektert belastning på 13,2 Kohm til rørene.

Dette viser at transformatoren ikke har noen egen impedans; resultatet er avhengig av omsetningsforholdet.

Selv om dette er den vanlige metoden som brukes for å beregne en push-pull-transformator, er a-a-impedansen ikke impedansen hvert rør ser når vi bruker forsterkeren, mer om det litt senere.

La meg ta et annet eksempel, vi skal lage en effektforsterker med 2 stk EL34 pentoder i push-pull kobling. Vi skal bruke katode bias og 450 volt som anodespenning. Hvis vi ser i data-arket fra Mullard, skal belastningen (Zaa) være 6.5 Kohm, og hvilestrømmen i hvert rør skal være 60 mA.

Maks signalstrøm (AC) skal være 71.5 mA og utgangseffekten blir da 40 W.

La oss regne ut omsetningsforholdet til denne transformatoren:

n = √(Rp/Rs) = √(6500/8) = 28.5

Vi må også sjekke at den transformatoren vi velger kan takle spenningen og maks strømmen i rørene. Transformatoren ovenfor fra Torodiy vil i dette tilfelle passe.

Spesifikasjonen fra produsenten er 6.6 Kohm, under vanlige forhold, så beregningen er riktig. Dette løser beregningen av omsetningsforholdet når det gjelder belastningen på sekundærsiden, men vi har også noen tap i transformatoren som bør tas i betraktning. La oss se på tapet på grunn av motstanden i kobbertråden i selve transformatoren.

Primær DC-motstand:

La oss introdusere likestrøms motstanden:

Når det ikke er signal, ser røret bare likestrømmotstanden til den primære viklingen (faktisk halvparten av den totale primære viklingen i et push-pull-trinn, i det minste i et klasse B-trinn). Så snart et vekselstrømsignal er til stede, vil imidlertid røret se likestrømmotstanden til primærviklingene i transformatoren i serie med den reflekterte impedansen fra lasten.

La meg ta et eksempel, og for dette eksempelet vil gå tilbake til SE trinn, det fungerer på samme måte, bare forestill deg at dette er halvparten av push-pull trinnet, som ser halvparten av transformatoren:

I dette eksemplet sier vi at DC-motstanden til den primære viklingen er 200 ohm (R1) (det er en veldig dårlig transformator, men den bare for å vise hvordan den fungerer); tegning “a” ovenfor viser tilstanden uten signal, røret ser bare motstanden til den primære kobberviklingen, presentert av R1 på tegningen. Dette er motstanden som brukes for å trekke lastlinjen for likespenning, hvilestrøm, uten signal til stede.

Når vekselstrømsignalet er til stede, vil det gå vekselstrømmer i transformatoren, og røret ser ikke bare 200 ohm, men også den reflekterte sekundære impedansen (n² x R2) i serie med den. Hvis vi setter “n” til å være 14 og høyttaleren til å være 8 ohm n² x R2 = (14) ² x 8, er den reflekterte impedansen 1568 ohm. Den totale AC-belastningen som røret ser, er da 1568 + 200 = 1768 ohm.

DC-belastningen som presenteres for røret er 200 ohm, og AC-belastningen er 1768 ohm.

Vi har ikke tatt hensyn til resistansen i sekundærviklingen i formelen, men den reflekteres sammen med høyttalerimpedansen. Den er som regel veldig liten og vil derfor ha mindre betydning.

Hvis vi ser på dataene for en ekte transformator ovenfor, er DC-motstanden til primærviklingen bare 96 ohm, og motstanden for sekundærsiden vil alltid være mindre enn dette, de normale toleransene for forskjellige rør (ri-variasjon) er mye større enn dette. Derfor vil det i den virkelige verden ikke gjøre noen merkbar forskjell om det er inkludert i beregningene eller ikke, bortsett fra når vi ønsker å tegne likestrøms lastlinjen, eller av selvfølgelig hvis vi designer en transformator, men det er ikke emne for denne artikkelen.

Vi har også andre tap i en utgangstransformator, blant dem er:

Effekt tap på grunn av magnetfeltet, dette er tap av hysterese og «eddy current (virvelstrøm)», dette er blant hovedårsakene til at en transformator for en SE-forsterker må være mye større enn for en P-P-forsterker, med lignende spesifikasjoner. Det er noen flere, tap for lav- og høyfrekvensområdet, disse avhenger av den fysiske konstruksjonen og utformingen av transformatoren, men ingen av dem vil bli behandlet i denne artikkelen.

Triode push-pull trinn:

Figur 1

push-pull-utgangstrinnet vil fungere annerledes i klasse A enn det ville gjort i klasse B, når det gjelder hvordan transformatoren brukes, med klasse AB et sted mellom disse. La oss se på operasjon i klasse A, men først en annen tegning for å forklare ting.

Denne tegningen er en såkalt ekvivalent krets til utgangstrinnet. Følgende er nye på denne tegningen:

ri Intern dynamisk motstand til røret (rp i usa) (AC-verdi)

Rp – Primær kobbermotstand

Rs – Sekundær kobbermotstand

Ns – Sekundærens antall viklinger

Np – Primærens antall viklinger

Zs – Sekundær belastningsimpedans

0,5 x Np er svingene for halvparten av primæren (a til a), for transformatoren, og 0,5 x Rp er halvparten av den totale kobbermotstanden til primæren, det vil være viktig senere. Alt til venstre for de svarte prikkene er internt i selve røret.

La oss først se på hva som skjer i et klasse A trinn:

I et klasse A-trinn vil begge de primære viklingene (0,5 x Np) lede seg samtidig, men i motsatt fase. Dette vil forårsake en sekundærstrøm siden primærhalvdelene vikles i motsatt retning. Nå vil impedansen til transformatoren som blir presentert for rørene være:

Husk at rørene bruker begge primære halvdeler samtidig:

Vi kan gjøre det litt enklere:

I tillegg, enda enklere hvis vi ikke tar kobber tapet til beregningen, og dette er formelen man vil bruke i de fleste tilfeller:

Belastningen (anodeimpedansen) til hver triode vil være, uten å ta hensyn til tap i viklingene:

Nå til triode push-pull forsterker i klasse B:

Her leder de primære transformatorhalvdelene anodestrømmene vekselvis. Hver triode leder eller blokkerer vekselvis, så her har vi bare en halv primær side i bruk av gangen.

Belastningen til hvert rør, uten all matematikken som leder fram til den, er:

Dette er for trioden som leder, den andre trioden blokkerer og har Za = ꝏ, men anodespenningen endrer seg fortsatt. Lastimpedansene pr. Triode i klasse B varierer mellom 0,25 ganger Zaa til og med Za, til uendelig avhengig av signal, eller satt på en annen måte:

0,25 x Zaa <Za <ꝏ

Klasse AB ligger et sted mellom A og B. og belastningsimpedansen pr. Triode varierer mellom:

0,25 x Zaa <Za <0,5 x Zaa

Vi kan si at belastningen som transformatoren presenterer for rørene ikke har en konstant verdi for alle strømverdier gjennom transformatorviklingene. I tillegg gjelder dette også den interne AC-motstanden i rørene (ri).

Dette viser at den dynamiske (AC) belastningslinjen for et utgangstrinn faktisk aldri vil være en rett linje, det er faktisk en ellipse, men vi kan ikke bruke den til praktiske beregninger, så vi antar at belastningen er en ren resistans og det gir oss et resultat vi kan bruke i praksis.

Når det gjelder valg av last for et gitt sett med rør, må det gjøres mange forskjellige kompromisser og valg. Jeg anbefaler å sjekke produsentens data, i hvert fall som et utgangspunkt.

Selv om jeg har presentert formlene ovenfor for et triodetrinn, er de også gyldige for et pentodeutgangstrinn.

Når vi spesifiserer en utgangstransformator for en forsterker, spesifiserer vi vanligvis belastningsimpedansen som anode til anode (a-a) (eller du kan bruke omsetningsforholdet), men vi må også spesifisere den maksimale anodestrømmen du forventer at utgangsrørene skal trekke.

Det er mye mer å si om utformingen av push-pull effektforsterkere og transformatorer, men det er ikke temaet for denne artikkelen. Blant de tingene som ikke er dekket, er komposittbelastningslinjer, B.J Thomson-metoden for lastelinjer, mest gunstig last og mye annet. Noen av dem vil bli gjenstand for en senere artikkel.